パチンコの立ち回り管理カテゴリー前回のブログ記事では、パチンコの出玉数とボーダーラインの関係について説明しました(前回のブログ記事「パチンコの出玉数とボーダーライン」はこちら)。今回はパチンコの期待収支計算に必要なトータル大当たり回数の計算方法について説明します。
パチンコを1日打った時の期待収支を計算するのに、1日のトータル出玉が必要になります。トータル出玉は大当たり時の平均出玉にトータル大当たり回数を掛ければ得られます。平均出玉数は前回の記事で説明しました。トータル大当たり回数については、これまでの立ち回り管理カテゴリーの記事で説明してきた1日当りの平均初当たり回数に平均連チャン回数を掛けることで単純に平均回数を計算することができます。ただし、1日のトータル大当たり回数は、当然、平均回数を中心としてばらつきを持ちますので、収支のばらつきを計算するのにトータル大当たり回数の確率分布を知る必要があります。
では、トータル大当たり回数の確率分布を計算するための数式を説明します。総回転数をn(時短中は除きます)、n回転デジタルを回した時の初当たり回数をX、初当たり確率をP、連チャン継続率をPcとすると、総回転数n回転でトータル大当たり回数がHt回になる確率P(Ht)は以下の式で表されます。
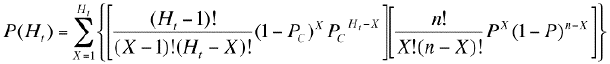
この式はHtが1回以上の場合に用います。Htが0回の時に限り、以下の式で確率を計算します。
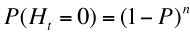
また、Htが総回転数nより大きいケースを計算する時は、若干計算式を修正する必要がありますが、丸1日パチンコを打って大当たり回数が総回転数を超えることはまずあり得ませんので、ここでは説明しません(1000円だけ打って、まぐれで何回大当たりを引けるかといった計算を行う場合には修正が必要です)。Htの平均値Htaveと標準偏差σHtは以下の式で与えられます。
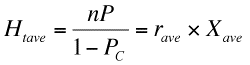
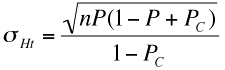
平均大当たり回数Htaveは前述のように平均連チャン数raveと平均初当たり回数Xaveを掛け合わせると得られます。標準偏差σHtは大当たり回数の分布幅を決める非常に重要な値です。大当たり回数はσHtの6倍の範囲にほとんど分布すると憶えておいてください。
さて、非常に複雑な数式です。数式を見ただけでは、Htの確率分布がイメージできまませんので、実際に計算した例を次に示します。
下のグラフは大海物語M56を1日打った時のトータル大当たり回数の確率分布を表しています。総回転数n は2500回転で計算しています。グラフの縦軸の値に100を掛けるとパーセントになります。
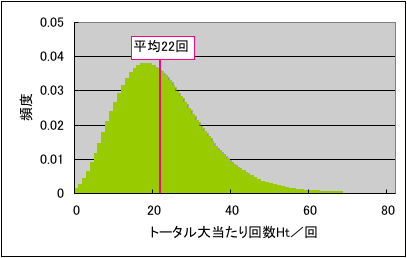
トータル大当たり回数が0回から60回くらいまで幅広い範囲に分布しているのがわかります。標準偏差σHtを計算すると11.1回になりますので、大当たり回数は前述のようにσHtの6倍くらいの範囲に分布しています。分布はHtの大きい方へ、しっぽが伸びたような形になっています。いわゆる、ロングテールを持った分布になっています。また、平均大当たり回数は以前の記事で説明した大海物語M56の平均初当たり回数と平均連チャン数から22回となりますが、分布のピークからかなりずれています。このような分布は、波の荒い機種の特徴的な形です。どういうことかと言うと、分布のピークが平均値より少ない回数側にあるということは、大海物語M56を1日打った場合に、トータル大当たり回数が平均回数以下で終わる確率が、平均回数を超える確率よりも高いことを示してします。グラフの分布ではトータル大当たり回数が平均回数以下になる確率は約56%です。ですから、もし大海物語M56で回転率がボーダーラインの台を1日打った場合、勝率は44%になります。一方で、トータル大当たり回数の分布は、平均値の2倍を上回る50回以上の領域まで裾野が広がっています。つまり、この形の分布は、ロングテールの部分が平均値を分布のピークより多い回数側へ引き上げている分布なのです。ですから、大海物語M56は普段は勝率が悪いけれど、たまに爆裂することで収支が上がる、リスクが高い台であると言えます。分布を見てみると大当たり回数が0回になる確率が約0.1%あります。大海物語M56を丸1日1000人が打ったとすると、一人くらいは一度も大当たりを引けずに終わってしまうことになります。金額にすると約15万負けになってしまいます。逆に大当たり回数が50回以上になる確率は約1%になります。50回と言うと等価交換で20万勝ちくらいになると思います。大海物語を丸1日100人が打ったとすると、一人くらいは20万以上勝つラッキーな人がいることになります。また、別の言い方をすると、毎日のように大海物語を打っていれば年に2、3回は誰でも20万以上の大勝ちをする可能性があるということです。このように大海物語M56のトータル大当たり回数の分布を見てみると、1日の期待収支にかなり幅があることがわかります。
もう1機種、デジハネのスーパー海物語SAEの計算結果を示します。総回転数nは上記と同じ2500回転です。スーパー海物語SAEの基本スペックはこのカテゴリーの連チャン継続率の記事で紹介しています。
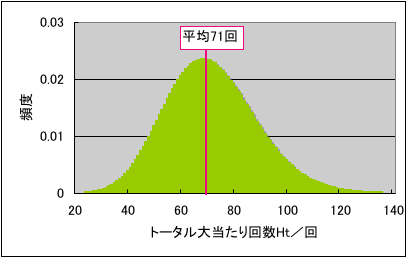
先ほどの大海物語M56に比べると、左右対称の確率分布になっています。これはスーパー海物語SAEの初当たり確率が高く(大海物語M56の約4倍)、確率分布が正規分布に近づくためです。スーパー海物語SAEで回転率がボーダーラインの台を1日打った場合、勝率は約48%と大海物語M56に比べると50%に近くなります。大海物語M56の場合でも、2週間とか1ヶ月くらいの期間で大当たり回数の分布を取ると、正規分布の左右対称の分布に近づいていきます。スーパー海物語SAEは大海物語M56に比べて、より短期間で収支が期待収支に収束すると言えます。標準偏差σHtを計算すると17.2回になります。トータル大当たり回数は平均値71回±50回くらいの範囲に分布してますので、分布幅はやはりσHtの6倍くらいになります。大海物語M56の時と違って、さすがにこの台を丸1日打って1回も大当たりを引けない人はいないでしょう。分布の幅が±50回ですから、大海物語M56に比べると大当たり回数の分布幅は広いですが、平均値に対する分布幅の比率で比較すると、約半分まで小さくなっています。おそらく期待収支の分布幅も大海物語M56の半分程度になるはずです。
以上、パチンコのトータル大当たり回数の確率分布について説明しました。次回の記事では、今回説明したトータル大当たり回数の確率分布を使って、パチンコの期待収支を計算します。
今日はここまで。

