パチンコの期待収支計算（前編）：パチンコ立ち回り管理に必要な知識

　パチンコの立ち回り管理カテゴリー前回のブログ記事では、パチンコのトータル大当たり回数の計算方法について説明しました（前回のブログ記事「パチンコのトータル大当たり回数の確率分布計算」はこちら）。今回はパチンコの期待収支計の計算方法について説明します。

　パチンコの期待収支を計算するには、トータル出玉とトータル消費玉数を計算する必要があります。トータル出玉は前回の記事で説明したトータル大当たり回数に大当たり時の平均出玉を掛けると求まります。数式で書くと、総回転数n回転でトータル大当たり回数がH_tだったとき、その機種の大当たり時の平均出玉をD_aveとすると、トータル出玉D_tは次ぎの式で表されます。

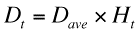
　次にトータル消費玉数ですが、これは台の回転率から計算します。回転率がxの台では1000円分の玉数250個消費する毎にスタートチャッカーにx個の玉が入賞することになります。と言うことは、デジタルを1回転させる度に250/x個の玉を消費することになります。したがって、総回転数n回転(時短中を除く）でのトータル消費玉数D_ltは以下の式で表されます。

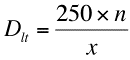
　トータル出玉D_tとトータル消費玉数D_ltから差玉が計算できます。差玉D_dは以下の式の通りです。

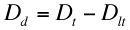
等価交換の場合、D_dに玉1個の金額4円を掛ければ、総回転数n回転消化した時点での収支になります。当然、差玉D_dがプラスならプラス収支、マイナスならマイナス収支になります。ここまでの数式を総合すると、回転率xの台を総回転数n回転消化した時点で、トータル大当たり回数がH_tだったときの収支Bは以下の式で表されます。

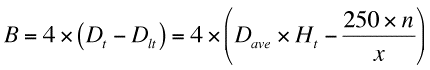
　平均期待収支を計算する場合には、この式のH_tに前回の記事で説明した平均トータル大当たり回数H_taveを入れれば計算できます。期待収支のばらつき（分布幅）を計算する場合は、Bの確率分布を計算する必要があります。上の式の中でH_t以外のパラメーターは、パチンコを打つ時の条件で定数です。したがって、収支がBになる確率は、前回の記事で説明したH_tの確率分布の式P(H_t)そのものになります。したがって、期待収支の標準偏差σ_Bは、前回の記事で説明したH_tの標準偏差σ_Htを用いて次の式で表されます。

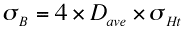
σ_Bは打つ機種のスペックだけで決まる値で、回転率には依存しません（回転率が変化しても大当たり時の出玉が変化しないという前提で計算する場合です。厳密には回転率が変化すると大当たり時の出玉も変化するのですが、その変化は微々たるものなので収支計算では無視します）。期待収支の分布幅はσ_Bの6倍の範囲にほとんど収まると憶えておいてください。

　それでは、実際に収支Bの確率分布を計算した例を紹介します。大海物語M56とスーパー海物語SAEについて、等価交換店で１日打ったときの収支の分布を計算した結果をグラフで示します。総回転数nは2500回転で計算しています。グラフの縦軸の値に100を掛けるとパーセントになります。また、グラフは回転率がボーダーライン(BL)-2回転、ボーダーライン(BL)、ボーダーライン(BL)+2回転の３つのケースについて計算した結果を示しています。ちなみに等価交換での大海物語M56のBLは16.6回転(D_ave=1700個として計算)、スーパー海物語SAEのBLは18.6回転(D_ave=470個として計算)です。

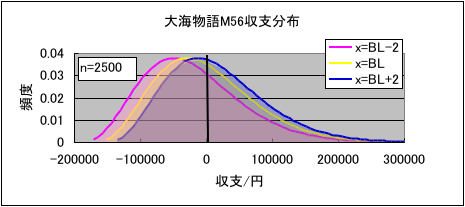
まず、大海物語M56についてグラフを見てみます。回転率xが大きくなると分布のピークがプラス収支側へ移動するのがわかると思います。つまり、回転率xが大きくなると勝率が高くなっていきます。各回転率の収支分布のピークがマイナス収支側にあるので、一見するとすべてのケースで平均収支がマイナスになるように思われます。しかし、平均収支がマイナスになるのはx=BL-2の時だけです。これは前回の記事でも書きましたが、分布のすそ野がプラス収支側に伸びていて、平均値が分布のピークよりもプラス収支側にずれるためです。収支はだいたい-15万円から+25万円くらいの範囲に分布しています。標準偏差σ_Bを計算すると75000円になりますから、収支がσ_Bの6倍くらいの範囲に分布しているのがわかります。各回転率での平均収支はx=BL-2のケースで-21000円、x=BLのケースで0円、x=BL+2のケースで+16000円になります。また、勝率（プラス収支になる確率）はx=BL-2のケースで34%、x=BLのケースで44%、x=BL+2のケースで55%です。回転率が大きくなると単純に勝率は上がりますが、x=BL+2でも45%の確率で負けてしまうわけですから、ボーダーラインを超えた台を１日打ったくらいではそれほど高い勝率にはならないことがわかります。逆にx=BL-2の台でも約1/3の確率で勝ちますので、回転率がボーダーラインを下回っていても勝つ可能性は十分にあります。これらの計算結果から、１日の収支はばらつきが大きく、回転率の差が収支に反映され難いということがわかります。このことは、グラフで各回転率の収支分布の大部分がオーバーラップしていることからも理解できると思います。

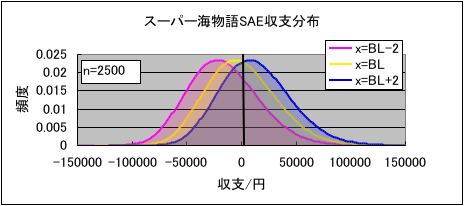
　次に初当たり確率が大海物語M56よりも約4倍高い、スーパー海物語SAEの収支の分布を見てみます。収支分布の幅は大体±10万円くらいの範囲に収まっています。標準偏差σ_Bを計算すると32000円になりますので、スーパー海物語SAEでも収支の分布幅はσ_Bの6倍くらいになります。大海物語M56に比べると分布の幅は半分くらいになります。各回転率の平均収支はx=BL-2のケースで-16000円、x=BLのケースで0円、x=BL+2のケースで+13000円になります。大海物語M56に比べると、勝ち負けどちらの場合も平均収支はやや小さい金額になります。勝率はx=BL-2のケースで29%、x=BLのケースで48%、x=BL+2のケースで64%です。前述の大海物語M56に比べると、回転率毎の勝率の差が大きくなっており、より回転率の差が反映された結果になっています。グラフを見ると各回転率の収支分布のオーバーラップしている範囲が、大海物語M56よりも少なくなっていることがわかると思います。このように大当たり確率が高く、平均大当たり回数が多くなるほど回転率の差が勝率に反映されるようになります。ただし、スーパー海物語SAEの場合でも、回転率がボーダーラインを超えた台を１日打ったくらいでは安定して勝てるという程の勝率にはなりません。

　今回の記事ではボーダーラインを基準に回転率と期待収支の関係を説明しました。ボーダーラインを基準とした回転率と期待収支の関係については以下のサイトの記事で詳しく説明していますので、参考にしてみてください。

ボーダーラインとパチンコの期待収支

　以上、パチンコの期待収支の計算方法とパチンコを１日打った場合の収支の計算例を説明しました。実際に収支の計算をしてみると、１日の収支はばらつきが大きく、高回転率の台を打ってもそれほど高い勝率にはならないことがわかってもらえたと思います。しかし、パチンコを打つ期間が１ヶ月、１年と言った長い期間になってくると、回転率による期待収支や勝率の差は歴然とした形で現れてきます。次回の記事では回転率による年間期待収支の差について説明したいと思います。

　今日はここまで。